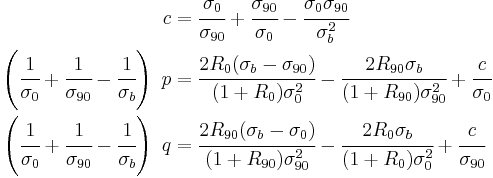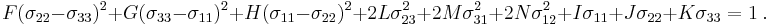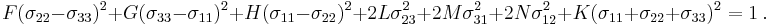Hill yield criteria
Rodney Hill has developed several yield criteria for anisotropic plastic deformations. The earliest version was a straightforward extension of the von Mises yield criterion and had a quadratic form. This model was later generalized by allowing for an exponent m. Variations of these criteria are in wide use for metals, polymers, and certain composites.
Contents |
Quadratic Hill yield criterion
The quadratic Hill yield criterion.[1] has the form
Here F, G, H, L, M, N are constants that have to be determined experimentally and 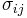 are the stresses. The quadratic Hill yield criterion depends only on the deviatoric stresses and is pressure independent. It predicts the same yield stress in tension and in compression.
are the stresses. The quadratic Hill yield criterion depends only on the deviatoric stresses and is pressure independent. It predicts the same yield stress in tension and in compression.
Expressions for F, G, H, L, M, N
If the axes of material anisotropy are assumed to be orthogonal, we can write
where 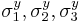 are the normal yield stresses with respect to the axes of anisotropy. Therefore we have
are the normal yield stresses with respect to the axes of anisotropy. Therefore we have
Similarly, if 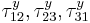 are the yield stresses in shear (with respect to the axes of anisotropy), we have
are the yield stresses in shear (with respect to the axes of anisotropy), we have
Quadratic Hill yield criterion for plane stress
The quadratic Hill yield criterion for thin rolled plates (plane stress conditions) can be expressed as
where the principal stresses 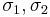 are assumed to be aligned with the axes of anisotropy with
are assumed to be aligned with the axes of anisotropy with 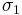 in the rolling direction and
in the rolling direction and 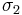 perpendicular to the rolling direction,
perpendicular to the rolling direction, 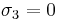 ,
, 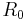 is the R-value in the rolling direction, and
is the R-value in the rolling direction, and 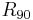 is the R-value perpendicular to the rolling direction.
is the R-value perpendicular to the rolling direction.
For the special case of transverse isotropy we have 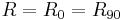 and we get
and we get
-
Derivation of Hill's criterion for plane stress For the situation where the principal stresses are aligned with the directions of anisotropy we have where
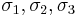 are the principal stresses. If we assume an associated flow rule we have
are the principal stresses. If we assume an associated flow rule we haveThis implies that
For plane stress
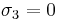 , which gives
, which givesThe R-value
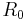 is defined as the ratio of the in-plane and out-of-plane plastic strains under uniaxial stress
is defined as the ratio of the in-plane and out-of-plane plastic strains under uniaxial stress 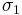 . The quantity
. The quantity 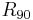 is the plastic strain ratio under uniaxial stress
is the plastic strain ratio under uniaxial stress 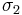 . Therefore, we have
. Therefore, we haveThen, using
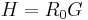 and
and 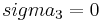 , the yield condition can be written as
, the yield condition can be written aswhich in turn may be expressed as
This is of the same form as the required expression. All we have to do is to express
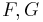 in terms of
in terms of 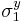 . Recall that,
. Recall that,We can use these to obtain
Solving for
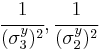 gives us
gives usPlugging back into the expressions for
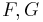 leads to
leads towhich implies that
Therefore the plane stress form of the quadratic Hill yield criterion can be expressed as
Generalized Hill yield criterion
The generalized Hill yield criterion[2] has the form
where 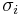 are the principal stresses (which are aligned with the directions of anisotropy),
are the principal stresses (which are aligned with the directions of anisotropy), 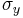 is the yield stress, and F, G, H, L, M, N are constants. The value of m is determined by the degree of anisotropy of the material and must be greater than 1 to ensure convexity of the yield surface.
is the yield stress, and F, G, H, L, M, N are constants. The value of m is determined by the degree of anisotropy of the material and must be greater than 1 to ensure convexity of the yield surface.
Generalized Hill yield criterion for plane stress
For transversely isotropic materials with  being the plane of symmetry, the generalized Hill yield criterion reduces to (with
being the plane of symmetry, the generalized Hill yield criterion reduces to (with 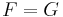 and
and 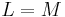 )
)
The R-value or Lankford coefficient can be determined by considering the situation where 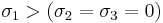 . The R-value is then given by
. The R-value is then given by
Under plane stress conditions and with some assumptions, the generalized Hill criterion can take several forms.[3]
- Case 1:
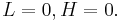
- Case 2:
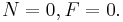
- Case 3:
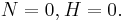
- Case 4:
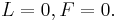
- Case 5:
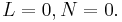 . This is the Hosford yield criterion.
. This is the Hosford yield criterion.
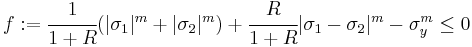
- Care must be exercised in using these forms of the generalized Hill yield criterion because the yield surfaces become concave (sometimes even unbounded) for certain combinations of
 and
and  .[4]
.[4]
Hill 1993 yield criterion
In 1993, Hill proposed another yield criterion [5] for plane stress problems with planar anisotropy. The Hill93 criterion has the form
where 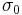 is the uniaxial tensile yield stress in the rolling direction,
is the uniaxial tensile yield stress in the rolling direction, 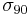 is the uniaxial tensile yield stress in the direction normal to the rolling direction,
is the uniaxial tensile yield stress in the direction normal to the rolling direction, 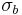 is the yield stress under uniform biaxial tension, and
is the yield stress under uniform biaxial tension, and 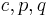 are parameters defined as
are parameters defined as
and 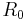 is the R-value for uniaxial tension in the rolling direction, and
is the R-value for uniaxial tension in the rolling direction, and 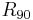 is the R-value for uniaxial tension in the in-plane direction perpendicular to the rolling direction.
is the R-value for uniaxial tension in the in-plane direction perpendicular to the rolling direction.
Extensions of Hill's yield criteria
The original versions of Hill's yield criteria were designed for material that did not have pressure-dependent yield surfaces which are needed to model polymers and foams.
The Caddell-Raghava-Atkins yield criterion
An extension that allows for pressure dependence is Caddell-Raghava-Atkins (CRA) model [6] which has the form
The Deshpande-Fleck-Ashby yield criterion
Another pressure-dependent extension of Hill's quadratic yield criterion which has a form similar to the Bresler Pister yield criterion is the Deshpande, Fleck and Ashby (DFA) yield criterion [7] for honeycomb structures (used in sandwich composite construction). This yield criterion has the form
References
- ^ R. Hill. (1948). A theory of the yielding and plastic flow of anisotropic metals. Proc. Roy. Soc. London, 193:281–297
- ^ R. Hill. (1979). Theoretical plasticity of textured aggregates. Math. Proc. Camb. Phil. Soc., 85(1):179–191.
- ^ Chu, E. (1995). Generalization of Hill's 1979 anisotropic yield criteria. Journal of Materials Processing Technology, vol. 50, pp. 207-215.
- ^ Zhu, Y., Dodd, B., Caddell, R. M. and Hosford, W. F. (1987). Limitations of Hill's 1979 anisotropic yield criterion. International Journal of Mechanical Sciences, vol. 29, pp. 733.
- ^ Hill. R. (1993). User-friendly theory of orthotropic plasticity in sheet metals. International Journal of Mechanical Sciences, vol. 35, no. 1, pp. 19–25.
- ^ Caddell, R. M., Raghava, R. S. and Atkins, A. G., (1973), Yield criterion for anisotropic and pressure dependent solids such as oriented polymers. Journal of Materials Science, vol. 8, no. 11, pp. 1641-1646.
- ^ Deshpande, V. S., Fleck, N. A. and Ashby, M. F. (2001). Effective properties of the octet-truss lattice material. Journal of the Mechanics and Physics of Solids, vol. 49, no. 8, pp. 1747-1769.
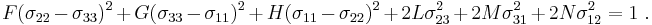
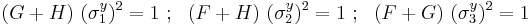
![F = \cfrac{1}{2}\left[\cfrac{1}{(\sigma_2^y)^2} %2B \cfrac{1}{(\sigma_3^y)^2} - \cfrac{1}{(\sigma_1^y)^2}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/446a20b5a7189aa7c309fdc3b150bbbe.png)
![G = \cfrac{1}{2}\left[\cfrac{1}{(\sigma_3^y)^2} %2B \cfrac{1}{(\sigma_1^y)^2} - \cfrac{1}{(\sigma_2^y)^2}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/a08b34a63efe61dad699fe334ceacacf.png)
![H = \cfrac{1}{2}\left[\cfrac{1}{(\sigma_1^y)^2} %2B \cfrac{1}{(\sigma_2^y)^2} - \cfrac{1}{(\sigma_3^y)^2}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/c4fd2f976410cabcb212cb70564e54a0.png)
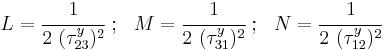
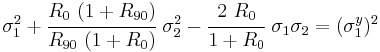
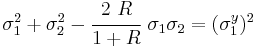
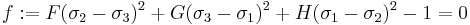

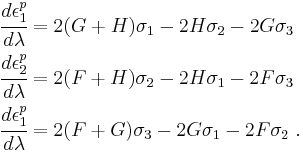
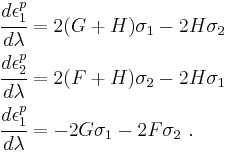
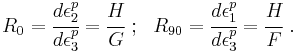
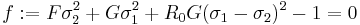
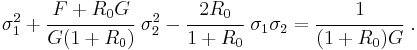
![\begin{align}
F & = \cfrac{1}{2}\left[\cfrac{1}{(\sigma_2^y)^2} %2B \cfrac{1}{(\sigma_3^y)^2} - \cfrac{1}{(\sigma_1^y)^2}
\right] \\
G & = \cfrac{1}{2}\left[\cfrac{1}{(\sigma_3^y)^2} %2B \cfrac{1}{(\sigma_1^y)^2} - \cfrac{1}{(\sigma_2^y)^2}
\right] \\
H & = \cfrac{1}{2}\left[\cfrac{1}{(\sigma_1^y)^2} %2B \cfrac{1}{(\sigma_2^y)^2} - \cfrac{1}{(\sigma_3^y)^2}
\right]
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/89c9b1512d7689bb5210246cfa08b372.png)
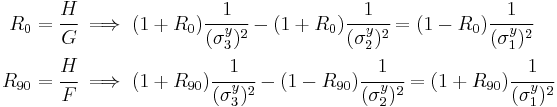
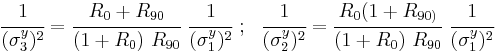
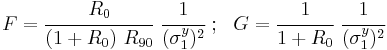
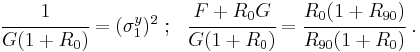
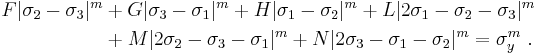
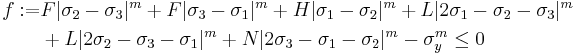
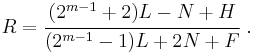
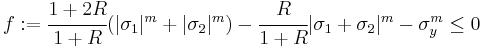
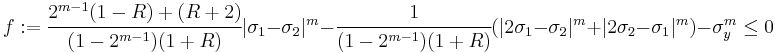
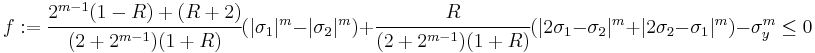
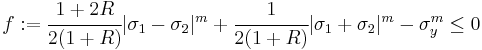
![\left(\cfrac{\sigma_1}{\sigma_0}\right)^2 %2B \left(\cfrac{\sigma_2}{\sigma_{90}}\right)^2 %2B \left[ (p %2B q - c) - \cfrac{p\sigma_1%2Bq\sigma_2}{\sigma_b}\right]\left(\cfrac{\sigma_1\sigma_2}{\sigma_0\sigma_{90}}\right) = 1](/2012-wikipedia_en_all_nopic_01_2012/I/e4b05afdc37ab45341a7c9c9bcbaaaf8.png)